Background: Understanding Physical Unclonable Functions (PUFs)
What are PUFs?
Physical Unclonable Functions (PUFs) are hardware-based security primitives that leverage the inherent manufacturing variations present in semiconductor devices. These variations, often microscopic and uncontrollable during fabrication, result in unique physical fingerprints for each device. PUFs exploit these variations to generate responses that are practically impossible to replicate, providing a reliable means of device authentication.
Importance in Hardware Security
PUFs play a crucial role in enhancing hardware security. Unlike traditional cryptographic methods that rely on stored secret keys, PUFs derive their security from the physical characteristics of the device. This makes PUFs resistant to various attacks, including invasive attacks attempting to clone or tamper with the device.
Applications of PUFs
- Device Authentication: PUFs can be used to authenticate electronic devices by generating unique identifiers based on their physical characteristics.
- Secure Key Generation: PUFs serve as a source of entropy for generating cryptographic keys, ensuring a high level of randomness and security.
- Anti-Counterfeiting: PUFs help combat counterfeiting by providing a reliable way to verify the authenticity of electronic components.
In the subsequent sections, we will delve into the implementation details of Arbiter PUF and Ring Oscillator (RO) PUF, highlighting their design principles, testing methodologies, and achieved results.
Introduction
In the realm of hardware security and trust, the implementation of Physical Unclonable Functions (PUFs) stands as a formidable solution. This blog explores the design and implementation of two distinct PUF variants: Arbiter PUF and Ring Oscillator (RO) PUF. The source code and project details can be found on GitHub.
Arbiter PUF: Harnessing Delay Differences
Design Overview
The Arbiter PUF relies on delay differences in multiplexers to generate unique responses based on challenge bits. Leveraging Verilog and ModelSim, we crafted a robust PUF architecture capable of handling a 4-bit challenge with 32-bit responses.
Implementation Details
To simulate the Arbiter PUF, we utilized the provided mux module with varying propagation delays. The 4-bit delay values for each multiplexer were parameterized using the DELAY parameter. The resulting PUF demonstrated an impressive single-chip Hamming distance of 49.10%, affirming its high-quality output.
Sub-Module Hierarchy and Design Decisions
Our design incorporated additional modules for a single response bit and a single round of the Arbiter PUF. The sub-module hierarchy was carefully crafted for modularity and scalability. The report details the design decisions made during the implementation.
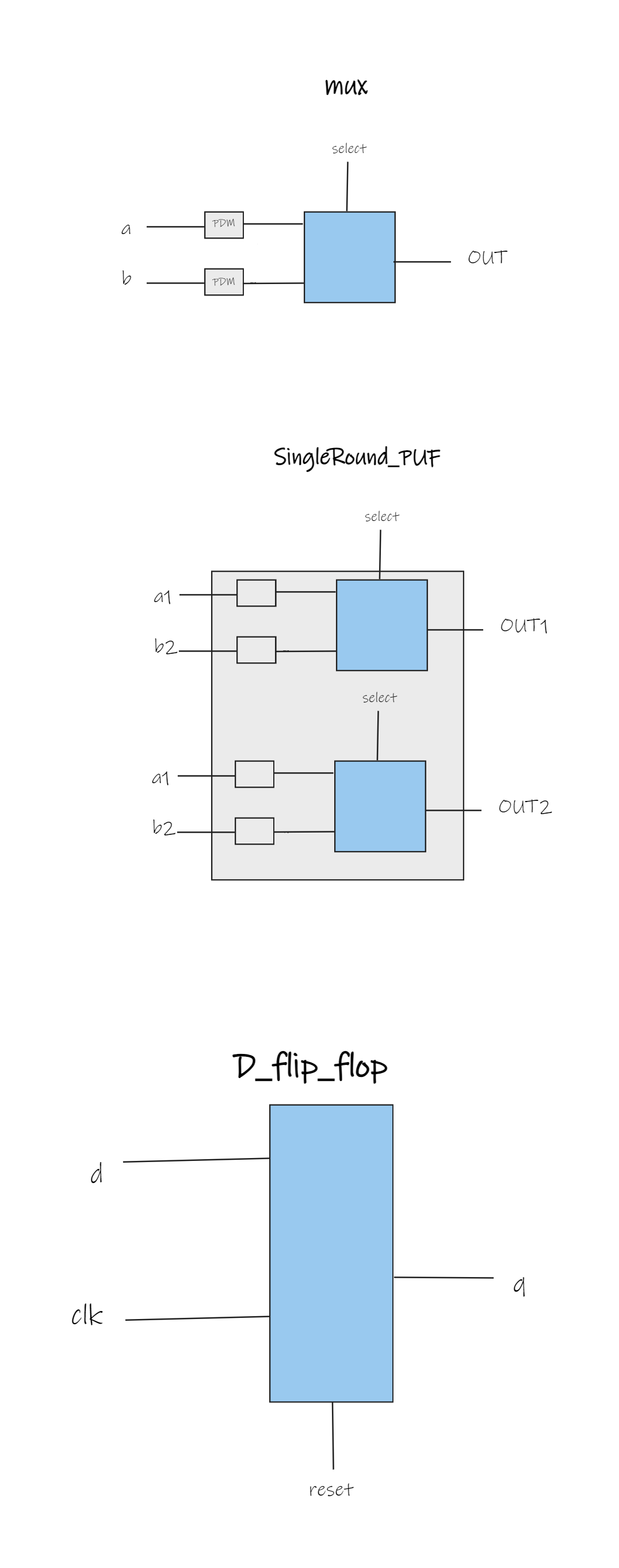
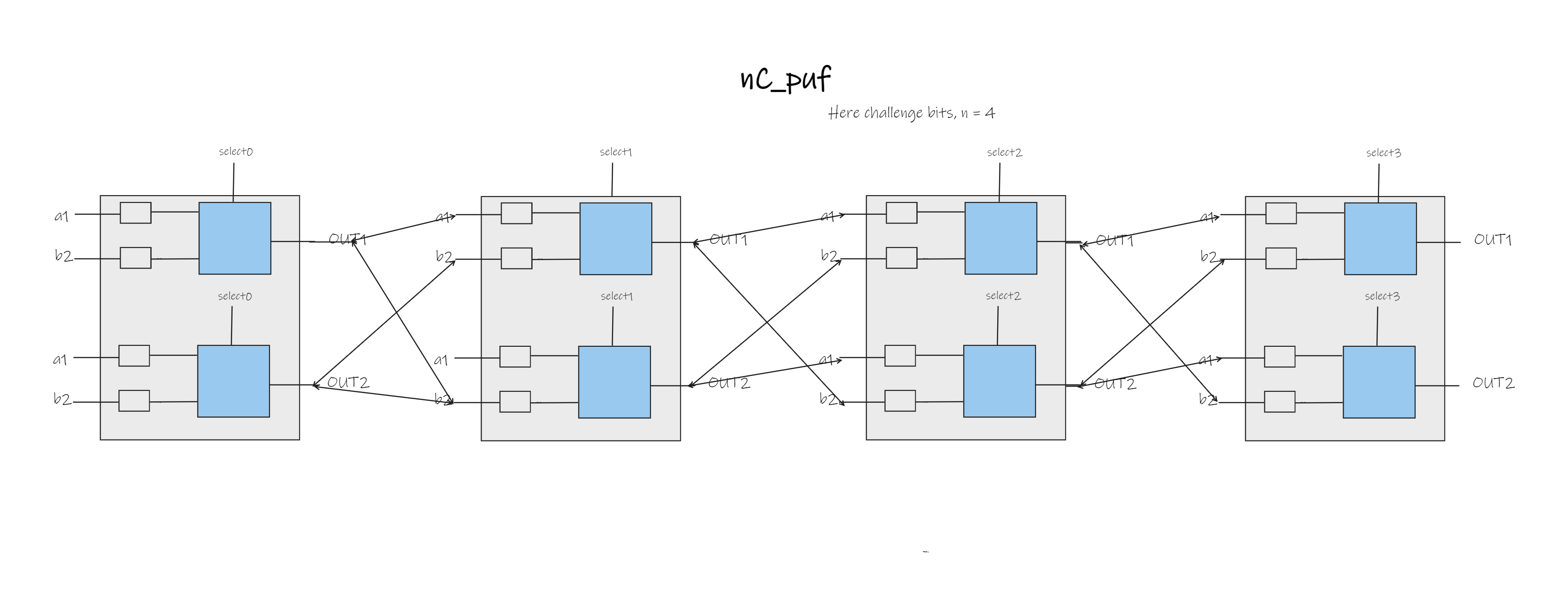
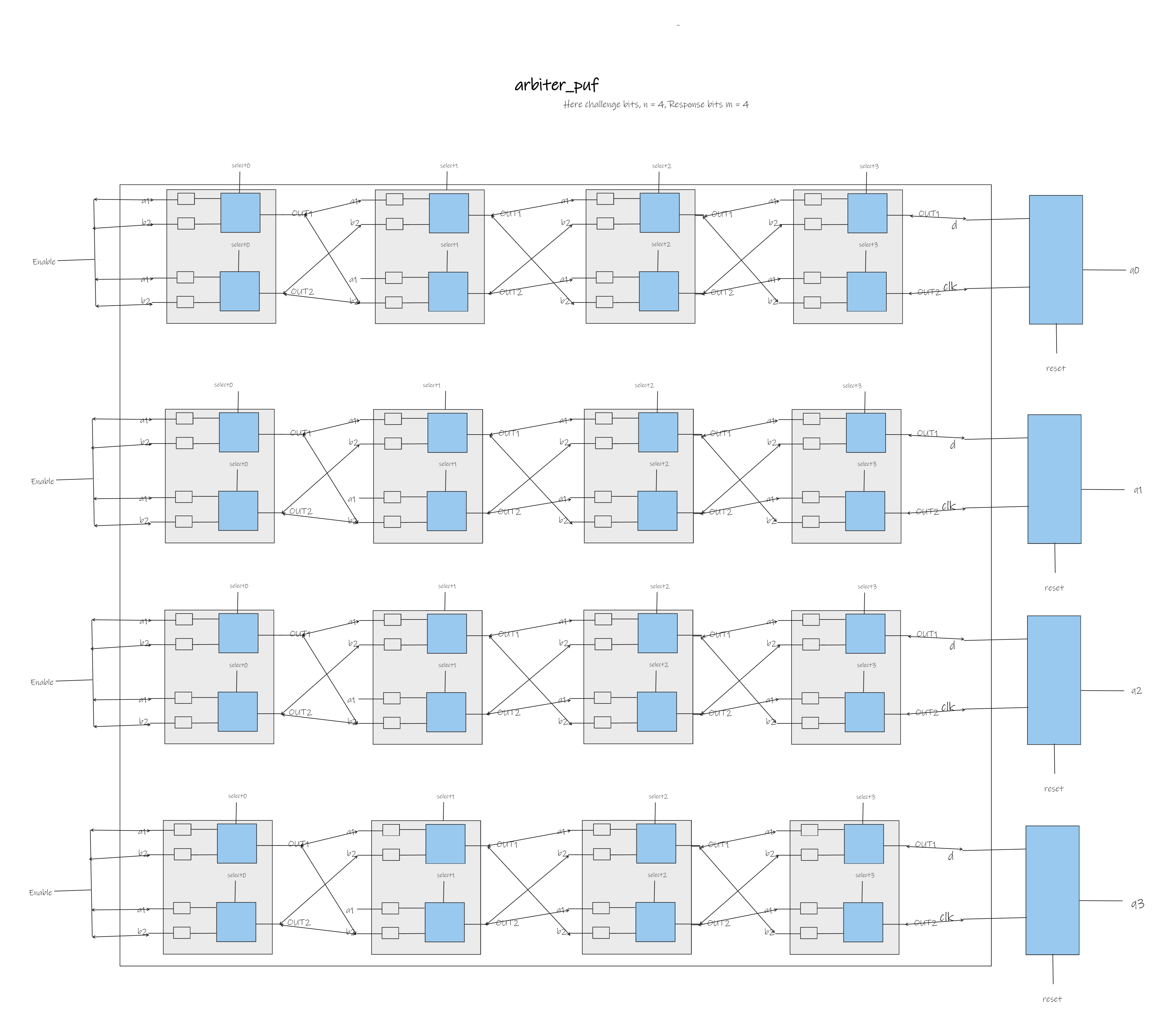
Verification and Testing
Ensuring the reliability of our PUF, we developed a comprehensive test bench for every module. The ModelSim GUI proved instrumental in observing signal waveforms and validating the functionality of the Arbiter PUF. The following table represents challenge-response pairs generated from random dealy parameter bits.
| Challenge | Response |
|---|---|
| 0000 | 11010110000010111010110011001011 |
| 0001 | 11011110001010010111110111011011 |
| 0010 | 01111111101000000101101101010010 |
| 0011 | 01110111010001011110101001010010 |
| 0100 | 00110101001001000101001101010000 |
| 0101 | 10110101000101001101001101010100 |
| 0110 | 11110100000001111011010101010001 |
| 0111 | 11110000000001000011110101010001 |
| 1000 | 00110001100101000101001100110100 |
| 1001 | 10100101000101111101001110110100 |
| 1010 | 10000000000111111011010110110101 |
| 1011 | 11011000000101110011010110110101 |
| 1100 | 11001100010010111010110010101011 |
| 1101 | 11011000100010110111110110101011 |
| 1110 | 00011111111110010101101110110010 |
| 1111 | 00000111010110011110101010100110 |
The resulting PUF demonstrated an impressive single-chip Hamming distance of 49.10%, affirming its high-quality output.
Ring Oscillator PUF: Unleashing FPGA Potential
RO PUF Architecture
Shifting focus to the RO PUF, our implementation targeted a Cyclone V GX FPGA. This variant employed multiple Ring Oscillators, each with unique frequencies due to fabrication variations. Challenge-Response Pairs (CRPs) were generated by racing counters using different RO outputs as clocks. We implemented RO PUF capable of producing 8-bit Challenge - 4-bit Response pairs. For a given 8-bit challenge - 1-bit Response PUF as shown below where N=16, 4 MSB from 8-bit challenge is used to select the ring oscillator for first MUX and the remaining 4 LSB for second MUX.
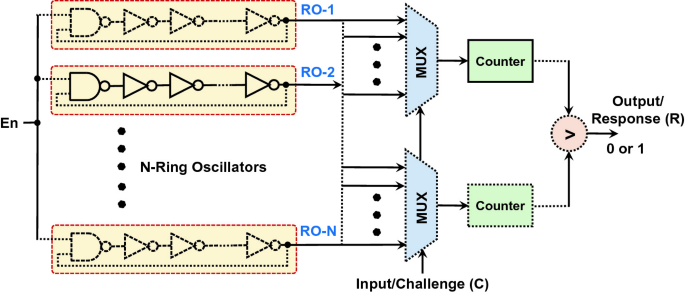
Synthesis and FPGA Integration
We utilized Quartus Prime to synthesize the Verilog design into an FPGA bit-stream. The Chip Planner tool facilitated the careful placement of RO modules within a single LAB Cell, minimizing propagation delays and ensuring optimal performance.
Results and Quality Assessment
The RO PUF exhibited a single-chip Hamming distance of 41.30% for 8-bit Challenge - 4-bit Response pairs, showcasing its robustness, while the utilizing 192 ALMS. The following table represents challenge-response pairs generated from FPGA.
| Challenge | FPGA Response |
|---|---|
| 00000000 | 1111 |
| 10001001 | 0101 |
| 01110011 | 1010 |
| 00001101 | 0011 |
| 11100101 | 0111 |
| 00110001 | 0101 |
| 01100110 | 1111 |
| 11000110 | 0111 |
| 11001000 | 1110 |
| 10000111 | 1010 |
| 00000011 | 1010 |
| 11110111 | 0101 |
| 10000001 | 0101 |
| 10111011 | 1111 |
| 00000001 | 0010 |
| 10100110 | 0001 |
| 11101011 | 1111 |
| 00010110 | 0011 |
| 10011111 | 1000 |
| 01000000 | 0101 |
| 00111100 | 0101 |
| 00101111 | 1010 |
| 01111100 | 1010 |
| 01010101 | 1111 |
Conclusion
This technical blog provides a comprehensive insight into the implementation of Arbiter PUF and RO PUF. The GitHub repository contains the complete source code and project files for further exploration. The achieved Hamming distances underscore the effectiveness of these PUF variants in generating unique and secure responses.
For detailed code snippets, project files, and a deeper dive into the implementation, visit our GitHub repository.
