In the realm of digital circuits, implementing mathematical functions efficiently is paramount for various applications, from signal processing to machine learning. In this technical exploration, we delve into the optimization of hardware implementations for one such crucial function: the exponential function .
Introduction
The task at hand involves implementing the exponential function for 16-bit fixed-point input values. While numerous methods exist for hardware realization, we opted for a Taylor expansion-based approach due to its simplicity and effectiveness. The 5th Taylor polynomial approximation serves as our foundation, providing a balance between accuracy and computational complexity.
Taylor Expansion of the Exponential Function:
The Taylor expansion of the exponential function is given by:
Baseline Implementation
Our journey begins with the baseline implementation, a fundamental circuit computed through Verilog. This circuit, rooted in the 5th Taylor polynomial, forms the cornerstone for subsequent optimizations. With a clear understanding of its functionality and performance metrics, we embark on the quest for enhancement.
Circuit Diagram:
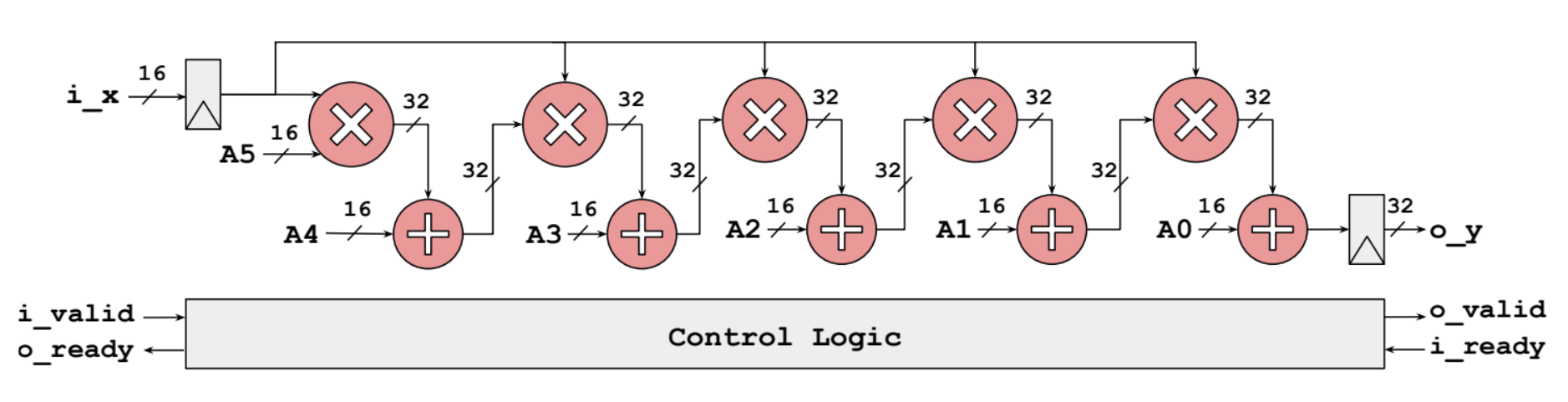
The Verilog code for the baseline implementation computes the 5th Taylor polynomial approximation of . It takes 16-bit fixed-point input values in Q2.14 format and produces 32-bit fixed-point outputs in Q7.25 format. The circuit consists of multipliers and adders arranged in a sequential manner to compute the polynomial terms and accumulate the result. Source code can be found here.
Pipeline Optimization
The first stop on our optimization journey leads us to the realm of pipelining. By introducing pipelines for multipliers and adders, we aim to enhance throughput and mitigate critical path delays. Leveraging registers strategically, we achieve a pipeline latency of 10 cycles, ensuring a steady stream of outputs with minimal overhead. Source code can be found here.
Pipeline Block Diagram:
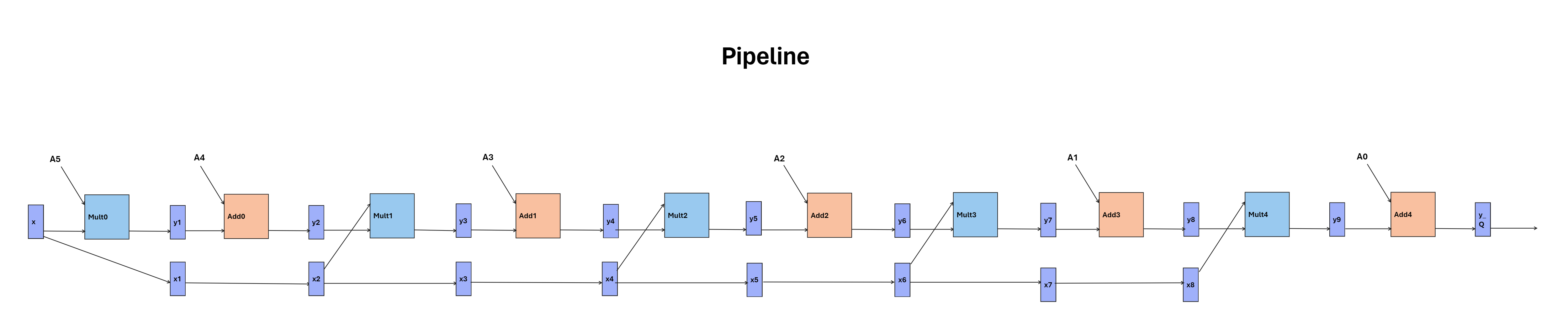
Thorough functional verification validates the efficacy of our pipelined design. Through waveform analysis and meticulous testing, we confirm the expected pipeline latency and ascertain the accuracy of our outputs.
Shared Hardware Design
In the shared hardware design, through the harmonious coordination of multipliers and adders orchestrated by a finite state machine (FSM), we aim to achieve optimal efficiency while maintaining high performance standards. Every input initiates a meticulously synchronized series of actions, resulting in outputs produced at regular intervals of 5 cycles. Source code can be found here.
Shared Hardware and FSM Diagram:
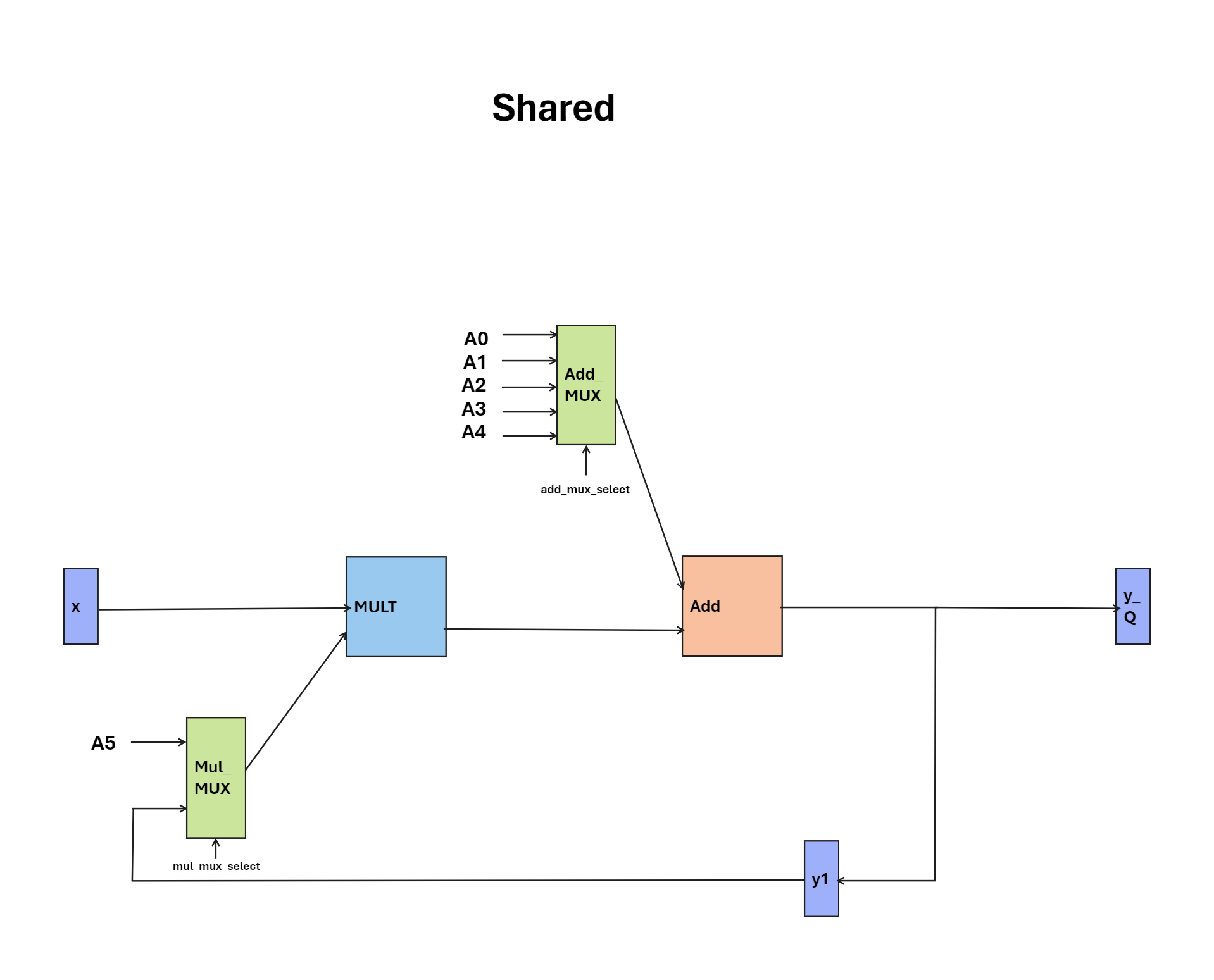
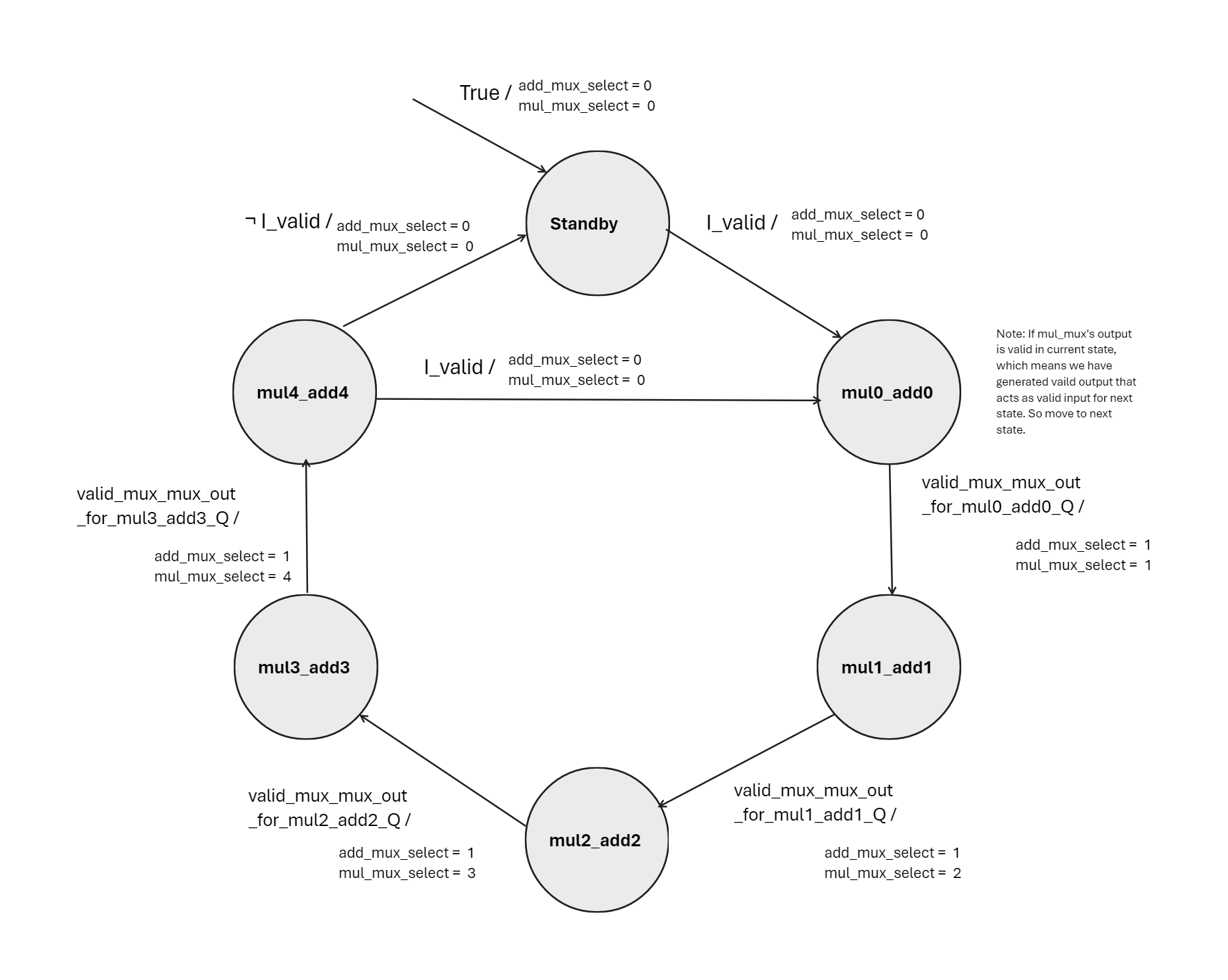
Comparative Analysis
With our optimized designs in hand, we conduct a comprehensive comparative analysis to gauge their efficacy. From resource utilization to operating frequency and throughput, each design undergoes meticulous scrutiny. The pipeline emerges as the champion in throughput, leveraging its enhanced frequency of operation to deliver unparalleled performance.
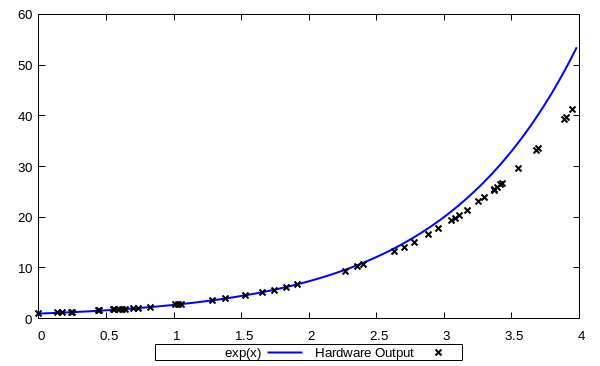
Exact vs. Approximated Exponential Function
As we are reimplementing same circuit for baseline, pipeline, and shared, we achieved same accuracy
Efficiency Metrics:
We calculate efficiency metrics for each design based on resource utilization, operating frequency, throughput, and dynamic power consumption. It's important to note that these metrics are calculated assuming the whole device is filled with maximum replications for a given circuit design, where the maximum DSP slices available are 1518.
| Metric | Baseline Circuit | Pipelined Circuit | Shared HW Circuit |
|---|---|---|---|
| Resources for one circuit | 36 ALMs + 6 DSPs | 92 ALMs + 4 DSPs | 34 ALMs + 2 DSPs |
| Operating frequency | 47.7 MHz | 213.35 MHz | 146.13 MHz |
| Critical path | DSP mult-add + 2x DSP mult + LE-based adder + 6x DSP mult + LE-based adder | Mult1 (2 ALMs) + Addr1 (1 ALM) + Mult2 & y4 (1 DSP) | State (1 FF) + multiplier’s mux (1 ALM) + Mult (2 DSPs) + Addr (1 ALM) + y_Q (1 FF) |
| Cycles per valid output | 1 | pipeline latency = 10, 1 cycle for every output after first output. | 5 |
| Max. # of copies/device | 253 (i.e. 1518 DSPs/6) | 379 (i.e. 1518 DSPs/4) | 759 (i.e. 1518 DSPs/2) |
| Max. Throughput for a full device (computations/s) | 12,068.1 Million computations/s (i.e. 253 * 47.7 MHz) | 80,859.65 Million computations/s (i.e. 379 * 213.35 MHz) | 22,182.534 Million computations/s (i.e. 759 * 146.13 MHz / 5) |
| Dynamic power of one circuit | 21.41 mW | 18.28 mW | 7.76 mW |
| Max. throughput/Watt for a full device | 2.23 billion computations/Watt (i.e. Max. Throughput/(21.41mW * 253 )) | 11.67 billion computations/Watt (i.e. Max. Throughput/(18.28 mW * 379 )) | 3.76 billion computations/Watt (i.e. Max. Throughput/(7.76 mW * 759)) |
Toggle Rate Analysis:
We also analyze the toggle rates for each design, which indicates how often signals change in the circuit.
| Circuit Design | Toggle Rate (Million Transitions/s) |
|---|---|
| Baseline | 134.086 |
| Pipelined | 129.790 |
| Shared HW | 140.558 |
Conclusion
In conclusion, our exploration into optimizing hardware implementations of the exponential function has yielded significant insights and effective strategies. We've observed that implementing a few terms of Taylor’s expansion leads to some level of inaccuracy, which can be mitigated by incorporating more terms for enhanced precision. Furthermore, while clipping the most significant and least significant bits during multiplication to fit the Q7.25 format introduces some loss of accuracy, widening inputs and outputs to achieve the desired precision before formatting to Q7.25 in the final stage can counteract this effect.
In terms of circuit efficiency, our analysis of toggle rates reveals that the pipelined design boasts the lowest toggle rate. Despite having larger circuitry than the other two designs, its lower toggle rate underscores its greater efficiency.
The pipelined architecture stands out for its ability to achieve the highest throughput, owing to the benefits of pipelining that allow for a higher frequency of operation and output generation. Compared to the baseline and shared designs, the pipelined approach excels in both frequency of operation and frequency of output generation.
