2 posts tagged with "C"

This blog aims to guide you through the process of programming a Pololu robot to execute a specific set of actions: ascending a ramp, recognizing the summit, changing direction, and safely descending the ramp without the risk of falling off. We will delve into best practices for designing an embedded system, breaking down the process into modeling, designing, and analyzing.

Throughout this journey, we'll navigate the intricacies of implementing line sensing, feedback control, and accelerometer integration to ensure our robot successfully ascends a ramp, executes a turn at the top, and descends without veering off the edge.

Background​

For this project, we will utilize Lingua Franca, the first reactor-oriented coordination language. It allows you to specify reactive components and compose them. Lingua Franca's semantics eliminate race conditions by construction and provide a sophisticated model of time, including a clear and precise notion of simultaneity. The blog will explain the concepts sufficiently for you to comprehend the program, even if you're not familiar with the language.

To kickstart our project, we'll fork lf-3pi-template, which comes with pico-sdk, facilitating a quick start.

Understanding the Task at Hand​

Our primary goal is to program the Pololu robot to perform a specific sequence: climb a ramp, detect the summit, turn around, and descend without falling off the edge. Key elements for this challenge include a ramp with a 15-degree slope, a flat turning surface at the top, a light-colored surface, and dark-colored edges for the robot to detect and avoid.

Modeling​

Let's initiate our project by modeling it with a finite-state machine and outlining the sensors we'll use.

Sensors Utilized​

Line Sensors​

For detecting edges and preventing the robot from falling off the wedge. Additionally, the accelerometer will provide roll, yaw, and pitch values, while the gyroscope calculates the angular velocity for precise turns.

Encoders​

Encoders play a crucial role in sustaining a consistent speed during both ascents and descents on the hill, effectively powering the wheels in accordance with the terrain.

Accelerometer​

Implement feedback control to adjust individual wheel speed periodically, maintaining a near-zero roll measurement. We will leverage the Motors With Feedback reactor to compensate for roll-induced variations in motor power.

Gyroscope​

Utilize the gyroscope to calculate angular displacement for accurate turning of the bot.

(Note: For more details about the implementation of the program for sensors, refer to the src directory)

Finite State Machine​

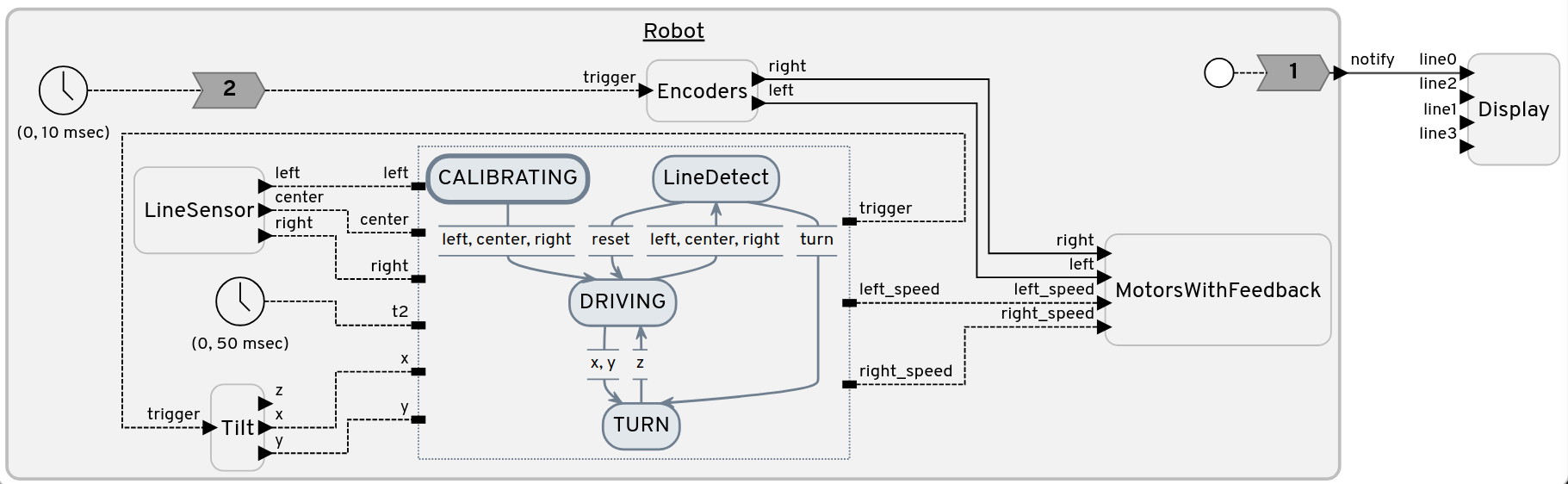
Our journey begins in a calibrating state, where we set the line sensor threshold. After a 5-second calibration, we transition to the driving state. Subsequently, the robot defaults to moving forward.

While moving forward, the robot may encounter the dark line or reach the end of the wedge. Upon detection, the robot saves the data, tracks back a few centimeters, and enters the LineDetect state. Decisions in this state are based on the saved data, leading to a 20-degree turn in the opposite direction of the detected line or a 180-degree turn if the wedge's end is detected.

Preparing for the Climb​

Before delving into the implementation, it's crucial to outline the key requirements for our robot program:

• Ascend and descend a ramp with a 15-degree slope.
• Detect dark-colored edges of the ramp using line sensors.
• Implement feedback motor control using accelerometer and encoders to adjust wheel speeds based on roll and encoder readings.
• Perfom precise turns using gyroscope measurements.

Designing/Implementation​

target C {
    platform: {
      name: "rp2040",
      board: "pololu_3pi_2040_robot"
    },
    threading: false,
  }
  
  import Display from "lib/Display.lf"
  import GyroAngle from "lib/IMU.lf"
  import LineSensor from "HillLineDetectSolution.lf"
  import Tilt from "lib/Tilt.lf"
  import Encoders from "lib/Encoders.lf"
  import MotorsWithFeedback from "lib/MotorsWithFeedback.lf";


  reactor Robot {
    output notify:string   // Notify of mode change.
    state turn_angle:int
    state turn_direction:int //+1 for left direciton, -1 for right direction
    state lineOnLeft:bool
    state lineOnCenter:bool
    state lineOnRight:bool
    state takenUTurn:bool=false


    lineSensor = new LineSensor()
    motors = new MotorsWithFeedback();
    encoder = new Encoders();

    encoder.right -> motors.right;
    encoder.left -> motors.left;

    tilt = new Tilt()
    timer t(0, 10 ms)
    timer t2(0, 50 ms)

    reaction(startup) -> notify {=
        lf_set(notify, "INIT:CALIBRATING");
      =}

    reaction(t) -> encoder.trigger {=
      lf_set(encoder.trigger, true);
    =}

    initial mode CALIBRATING 
    {
        reaction(lineSensor.left, lineSensor.center, lineSensor.right) -> reset(DRIVING), notify {=
            lf_set_mode(DRIVING);
            lf_set(notify, "DRIVING");
        =}
    }

  mode DRIVING { 

    reaction(reset) ->  motors.left_speed, motors.right_speed {=
      lf_set(motors.left_speed, 0.2); //0.2 m/s
      lf_set(motors.right_speed, 0.2);
    =}

    reaction(t2) -> tilt.trigger{=
        lf_set(tilt.trigger, true);
    =}

    reaction(tilt.x, tilt.y) ->  motors.left_speed, motors.right_speed, reset(TURN), notify {=

      if(tilt.x->value <= 0 && !self->takenUTurn)//considering  we have reached the top, then perfom U-turn
      {
        self->turn_angle = 180;
        self->turn_direction = 1;//direction doesn't matter
        self->takenUTurn = true;
        lf_set_mode(TURN);
        lf_set(notify, "TURN");
      }

      lf_set(motors.left_speed, 0.2 * (1.0 - 0.05 * tilt.y->value * ((tilt.x->value >= 0) ? 1.0 : -1.0))); 
      lf_set(motors.right_speed, 0.2 * (1.0 + 0.05 * tilt.y->value * ((tilt.x->value >= 0) ? 1.0 : -1.0)));

    =}

    reaction(lineSensor.left, lineSensor.center, lineSensor.right) -> reset(LineDetect), notify {=

      self->lineOnLeft = lineSensor.left->value;
      self->lineOnCenter = lineSensor.center->value;
      self->lineOnRight = lineSensor.right->value;
        
      if(self->lineOnLeft|| self->lineOnCenter || self->lineOnCenter)
      {
        lf_set_mode(LineDetect);
        lf_set(notify, "LineDetect");
      }
    =}
    }
  
  mode LineDetect {
    logical action turn    

    reaction(reset) -> motors.left_speed, motors.right_speed, turn, reset(DRIVING), notify {=

        lf_set(motors.left_speed, -0.2);
        lf_set(motors.right_speed, -0.2);

      if(self->lineOnCenter)
      { 
        self->turn_angle = 180;
        self->turn_direction = 1;//direction doesn't matter
        
      }
      else if(self->lineOnLeft)
      { 
        self->turn_angle = 20;
        self->turn_direction = -1; //right
      }
      else if (self->lineOnRight)
      {
        self->turn_angle = 20;
        self->turn_direction = 1; //right
      }
      else
      {
        //no line detected
        lf_set_mode(DRIVING);
        lf_set(notify, "DRIVING");
      }

      lf_schedule(turn, SEC(0.4));
    =}
  
    reaction(turn) -> reset(TURN), notify{=
      lf_set_mode(TURN);
      lf_set(notify, "TURN");
    =}

  }

  mode TURN {
    gyro = new GyroAngle()

    reaction(reset) ->  motors.left_speed, motors.right_speed {=
      lf_set(motors.left_speed, self->turn_direction * -0.2);
      lf_set(motors.right_speed,self->turn_direction * 0.2);
    =}

    reaction(t) -> gyro.trigger {=
      lf_set(gyro.trigger, true);
    =}

    reaction(gyro.z) -> reset(DRIVING), notify{=
    if(abs(gyro.z->value) > self->turn_angle)
    {   lf_set_mode(DRIVING);
        lf_set(notify, "DRIVING");
    }
    =}
  } 


  
  }
  
  main reactor {
    robot = new Robot()
    display = new Display()
    robot.notify -> display.line0;
  }
  

The primary component in the above Lingua Franca program is a reactor, functioning like an object to some extent. The reactor can have multiple states, and it provides mechanisms to transition between states based on time or physical/logical actions. It also has interfaces to input and output the data.

Here, in the program, we have two reactors:

1. Robot
2. Display

A Robot reactor has a total of 4 states:

1. CALIBRATING
2. DRIVING
3. LINEDETECT
4. TURN

The Robot reactor operates exclusively in one of its states at any given time. According to the design, the robot defaults to the CALIBRATING state and then shifts to DRIVING after completing the calibration process. The robot remains in the DRIVING state until it encounters obstacles. Upon detecting obstacles, it retraces a few centimeters, transitioning to the LINEDETECT state. In the LINEDETECT state, a decision is made to navigate around the obstacle. After deciding, it proceeds to the TURN state, determining the number of degrees to turn (let's say x degrees) and the direction (clockwise/anti-clockwise) based on information from LINEDETECT during exit.

Once the TURN state executes actions in line with the decision from LINEDETECT, control shifts back to the DRIVING state, with its default behavior of moving forward. Following the initial CALIBRATING state, the robot continually cycles through the DRIVING, LINEDETECT, TURN states to fulfill its designated task.

Finally, the Display reactor receives input from the Robot reactor to showcase obstacle detection, indicating positions such as left, right, and middle.

Analysis​

The robot effectively accomplishes its assigned mission, skillfully steering clear of the dark-colored edges. Moreover, the feedback control adeptly mitigates variations in roll, ensuring a consistent speed both uphill and downhill. Once aligned with the ramp, the robot seamlessly follows a straight path, courtesy of the precise adjustments made by the feedback control system. In instances where the robot starts its task atop the dark-colored edges, it promptly detects the situation and makes informed decisions to evade potential issues.

Conclusion​

This project seamlessly combines sensor integration, feedback control, and real-world navigation, offering valuable insights into the intricate challenges of robotics and a practical way to apply the concepts learned from embedded systems courses, including Designing, Modeling, and Analysis. Source code can be found at Github. Stay tuned for more exciting technical explorations in our upcoming blogs!

References​

• Edward A. Lee and Sanjit A. Seshia, Introduction to Embedded Systems, A Cyber-Physical Systems Approach Second Edition, MIT Press, ISBN 978-0-262-53381-2, 2017.
• Lingua Franca

Background: Fully Homomorphic Encryption Unveiled​

Before we embark on our comparative analysis of the SEAL and OpenFHE libraries, let's unveil the revolutionary concept of Fully Homomorphic Encryption (FHE). In the realm of cryptography, FHE stands as a beacon of innovation, allowing computations on encrypted data without the need for decryption.

Traditional encryption methods ensure the confidentiality of sensitive information during transmission or storage. However, they often hinder the ability to perform computations on this encrypted data without decrypting it first. FHE, on the other hand, transcends these limitations by enabling operations directly on encrypted data, preserving its confidentiality throughout the computational process.

Introduction​

In this technical blog, we delve into the world of FHE and conduct a comparative analysis of two leading open-source libraries: Microsoft SEAL and OpenFHE. Our exploration focuses on the implementation of two widely-used FHE schemes, Brakerski-Gentry-Vaikuntanathan (BGV) and Brakerski/Fan-Vercauteren.

Understanding OpenFHE and SEAL​

OpenFHE: A Glimpse into Versatility​

OpenFHE, powered by Duality Technologies, emerges as a versatile open-source homomorphic encryption library. Its popularity stems from its support for a diverse range of FHE schemes, including BFV, BGV, CKKS, FHEW, and TFHE. Additionally, OpenFHE incorporates multiparty extensions for threshold FHE and proxy re-encryption, providing a comprehensive toolkit for various cryptographic applications.

Explore OpenFHE: OpenFHE GitHub Repository

To download OpenFHE binaries, visit the OpenFHE GitHub Releases section.

SEAL: Harnessing Microsoft's Expertise​

SEAL, an open-source library developed by Microsoft, is designed to implement the most popular FHE schemes in use today: BGV, BFV, and CKKS. Leveraging Microsoft's expertise in cryptography, SEAL offers a robust platform for secure computations over encrypted data.

Explore SEAL: SEAL GitHub Repository

To download SEAL binaries, visit the SEAL GitHub Releases section.

Homomorphic Operations Data and Analysis​

For our comparative analysis, we leverage the resources available in the GitHub repository. The repository contains C programs and binaries, facilitating a more detailed and resourceful exploration.

The provided binaries include:

1. SEAL BGV
2. SEAL BFV
3. OpenFHE BGV
4. OpenFHE BFV

Each binary executes homomorphic addition and multiplication operations on encrypted data, producing runtime and result outputs. These binaries serve as the foundation for our exploration into the efficiency and performance of FHE schemes.

Data Generation and Analysis​

To initiate our analysis, we generate at least ten unique combinations of inputs for both multiplication and addition operations, taken average over ten iterations. The resulting tables showcase the runtimes of these operations for each scheme within the SEAL and OpenFHE libraries.

Pre-compiled binaries for the above libraries are provided at GitHub repository. To build you own binaries refer appendix. One can runs the binaries as follows.

./openFHE_BFV 1 1 2

Multiplication:​

Visualization for Enhanced Comprehension

Addition:​

Visualization for Enhanced Comprehension

Comparing the overheads when FHE is not used​

The GitHub repository also includes C programs that perform identical multiplication and addition operations on 64-bit integer values. The execution times are compared with FHE operations, revealing the overheads associated with FHE execution.

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <inttypes.h> 

int main(int argc, char *argv[]) {
int64_t num1, num2, num3;


if (argc >= 4) {
    num1 = strtoll(argv[1], NULL, 10);
    num2 = strtoll(argv[2], NULL, 10);
    num3 = strtoll(argv[3], NULL, 10);
} else {
    printf("usage: ./c_program <num1> <num2> <num3> \n");
    return 1;
}
   

int64_t add, mul;
clock_t start, end;
double add_time, mul_time;


start = clock();
add = num1 + num2 + num3;
end = clock();

add_time = ((double) (end - start)) / CLOCKS_PER_SEC * 1000; //time in milliseconds.


// Perform multiplication
start = clock();
mul = num1 * num2 * num3;
end = clock();
mul_time = ((double) (end - start)) / CLOCKS_PER_SEC * 1000; //time in milliseconds


// Output results
printf("mul_time: %lf   add_time%lf\n", mul_time, add_time);

return 0;
}

Multiplication:​

Average Overheads:

Addition:​

Average Overheads:

Conclusion​

Our analysis brings forth a compelling narrative. OpenFHE demonstrates superior implementation of FHE schemes, with OpenFHE_BGV emerging as the top performer, closely followed by OpenFHE_BFV. SEAL, while robust, exhibits higher runtimes compared to OpenFHE, suggesting that OpenFHE's implementation is more efficient.

Explore Further

To delve deeper into the world of homomorphic encryption and contribute to its advancements, consider exploring the GitHub repositories for OpenFHE and SEAL:

• Explore OpenFHE: OpenFHE GitHub Repository
• Explore SEAL: SEAL GitHub Repository

Download the respective binaries from the library repositories and engage in the evolving landscape of homomorphic encryption.

This exploration not only enhances our understanding of FHE but also contributes valuable insights to the ongoing development of secure and privacy-preserving computational technologies.

Appendix​

This section provides details on the build process for two libraries. The instructions are presented to facilitate independent experimentation with Fully Homomorphic Encryption (FHE) implementations.

Prerequisites​

To execute this project, ensure that the following dependencies are installed:

• CMake
• G++
• GMP
• Clang

OpenFHE​

Navigate to the openfhe directory and follow these steps to set up the project:

mkdir build
cd build
cmake ..
make
make install
make testall

After modifying the code, compile test programs using the following commands:

make added_bgv
make added_bfv

To execute the examples, run the binaries as follows:

bin/examples/pke/added_bgv
bin/examples/pke/added_bfv

Additionally, new files created will be automatically linked during the make process.

SEAL​

Set up this library with the following instructions:

cmake -S . -B build -DSEAL_BUILD_EXAMPLES=ON
cmake --build build
sudo cmake --install build

To run the compiled work, locate the binary at build/bin/sealexamples.